Pour comprendre Theorie de Froude relative aux hélices de captage et limite de betz la notion de quantité de mouvement doit etre maitrisée, car c'est sur le bilan de quantité de mouvement que la théorie de Froude s'appuie..

La méthode de Froude utilise les équations de conservation de quantité de mouvement pour déterminer les performances d'une hélice considérée comme étant un disque uniformément chargé ayant un nombre infini de pales.Les vitesses induites axiales peuvent ainsi etres évaluées

• La rotation de l'écoulement est négligée
• Le fluide est incompressible
• L'écoulement à I'extérieur de la veine traversant le disque est non perturbé
• La pression à l'infini en amont et en aval est égale à la pression statique de
  l'écoulement
• l'air passe a travers le rotor sans frottement

Le disque agit comme un frein opposant une force T au courant de fluide. Cette force peut etre considérée comme le resultat de la diférence de pression entre l'amont et l'aval du disque.

L'équation de continuite nous dit que, pour conserver un meme débit, si la vitesse diminue la section doit augmenter. Si nous observons le debit de la veine de fluide passant dans le disque, nous voyons donc la section augmenter par le freinage du fluide.

Observons notre hélice dans un volume de controle plus grand que la veine traversant l'hélice.Nous constatons que l'élargissement de veine ne peut se faire que si une certain volume de fluide est évacuée du volume de controle.

Figure 1

 

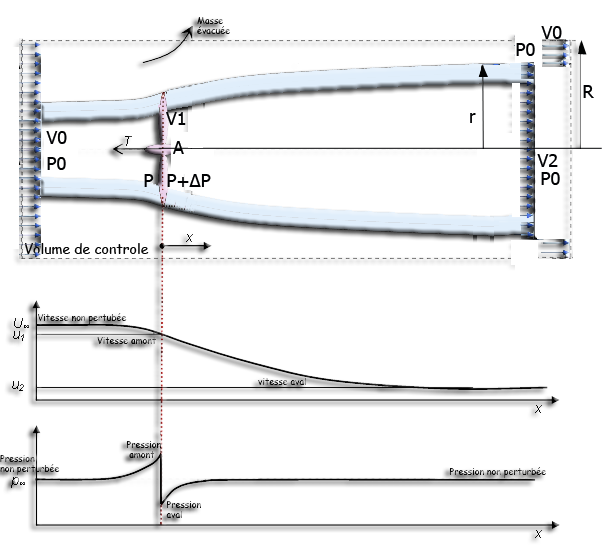
l'équation de continuité nous permet de calculer le volume évacué de la zone de controle par seconde (débit volumique Q en m3/sec),

 

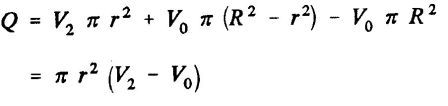
Q représente le débit volumique évacué du volume de contrôle. A partir du théorème de quantité de mouvement, on obtient la force de traction, T (ou de propulsion) de l'hélice, c'est-à-dire la variation de la quantité de mouvement entre les sections 2 et O, dont la projection sur l'axe horizontal indique la traction :

la dérivée de la quantité de mouvement par rapport au temps :

Quantité de mouvement "M_2" sortant du volume de controle à la section 2 =

 

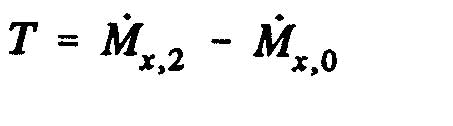
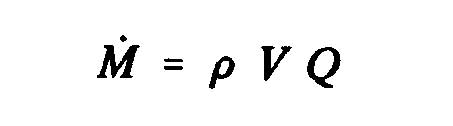
Quantité de mouvement total "M_1" entrant dans le volume de controle = Quantité de mouvement à l'entrée du volume - quantité de mouvement evacué latéralement=

Dès lors, la force axiale du fluide sur le rotor devient(T=M_2-M_1):

On peut également exprimer la force axiale du fluide sur le rotor T ,en regard de la résultante de la pression statique qui s'exerce sur la surface du disque:

où A est la surface du disque balayée par l'hélice et Dp, la différence de pression à travers le disque. Grâce à l'équation de Bernoulli, on obtient

de O à 1 en amont, et:

de 2 à 1 en aval.

 

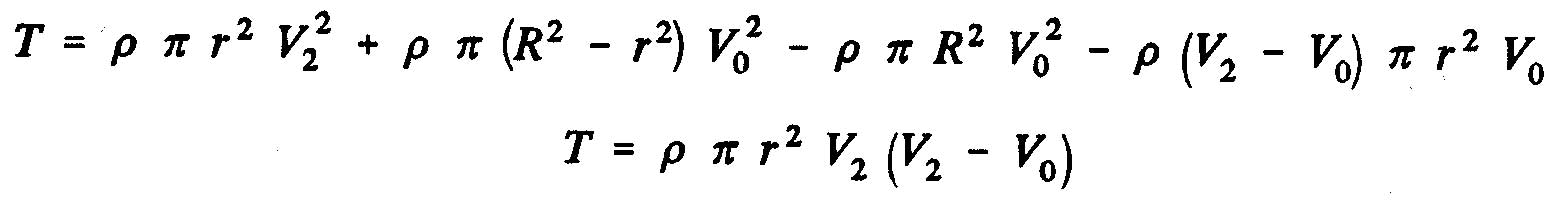
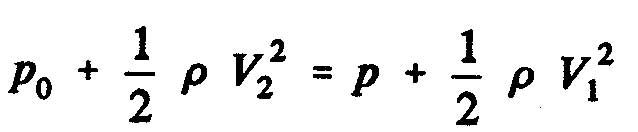
La différence de pression statique entre les faces aval et amont du disque de l'hélice a comme expression

De l'équation de continuité:, on peut tirer:

et considérer la vitesse de l'écoulement au niveau du disque comme une moyenne arithmétique des vitesses en amont et en aval de l'hélice:

La vitesse de l’écoulement de l’air à travers le rotor est la moyenne des deux vitesses celle en amont et celle en aval du rotor. On appelle vitesse induite, w, la diminution de vitesse au niveau du disque de l'hélice:

ou a représente le facteur d'interférence axiale.

 

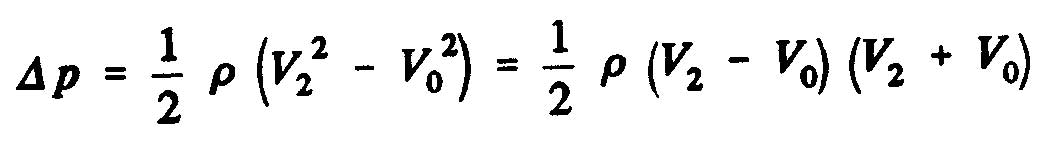
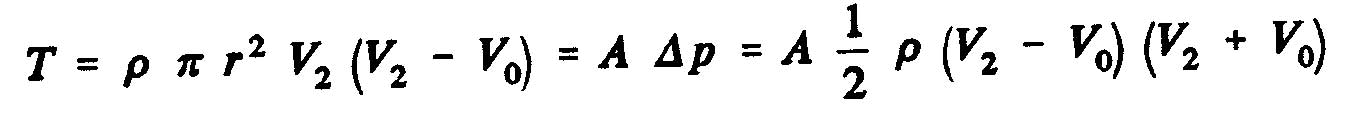
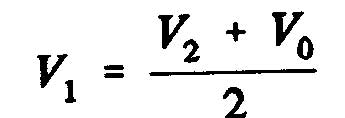
Maintenant, si on tient compte de l'expression:, la force axiale qui s'exerce sur le disque de l'hélice est :

La puissance extraite du vent est :

Le coefficient de puissance est défini comme le rapport entre la puissance disponible du vent et la puissance extraite :

Introduisant le facteur d’interférence axial a, défini comme la fraction de diminution de la vitesse du vent, entre celle de l’écoulement libre en amont du rotor et celle traversant le plan du rotor :

• V=(1-a).V0

En utilisant l’équation () :

• V1=(1-2a).V0

Sachant que:

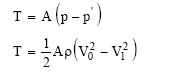
En substituant V1 et V , on obtient :

L’expression de Cp devient

La valeur maximale de théorique du coefficient de puissance, connue sous le nom de limite de Betz, peut être obtenue en prenant la dérivée de Cp par rapport à: a=0 ,

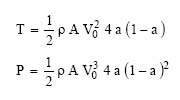
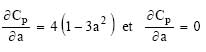
Cela donne :

Le rendement maximal pour une éolienne idéale est approximativement 59,3 %. Dans la pratique, ce rendement n’est jamais réalisé à cause des effets suivants :

• L’écoulement de l’air a une composante rotative due à la rotation du rotor.
• La force de traînée n’est jamais nulle à cause des frottements.
• L’hélice contient un nombre fini de pales.

Ce modèle simple unidimensionnel ne décrit pas l’écoulement rotatif de l’air, cependant il permet de définir certains concepts fondamentaux dans le fonctionnent des éoliennes.
Pour que l’hélice extrait l’énergie du vent, la vitesse de ce dernier doit diminuer lorsqu’il traverse l’hélice. Une machine idéale doit ralentir la vitesse du vent de 2/3.
D’après l’équation de continuité (1), la section de l’air balayé par le vent augmente de l’amont vers l’aval. Pour une éolienne idéale, l’aire de la section de l’écoulement à l’amont est de 2/3 celui du rotor, et ce dernier est la moitié de celui de la section en aval. Finalement, l’extraction de toute l’énergie disponible du vent est pratiquement impossible, dans la pratique, le rendement des éoliennes ne dépasse pas les 45 %.

 

La theorie de froude nous donne donc la vitesse induite axiale. Elle sera couplée à la théorie de l'élément de pale, pour donner une décomposition de la vitesse induite, en vitesses induites tangentielles et axiales, nécéssaires à la prediction des angles d'incidences et de la géometrie des pales

References bibliographique helice